een wiskundige knoop tekenen

Een touwtje knopen is deel van het alledaagse leven van mensen ongeveer overal op de wereld. Met een opeenvolging van lussen maken, uiteinde onder of boven een touw doen enzoverder heeft de mensheid een hoop knopen ontwikkeld. Het wiskundige interesse in knopen is echter veel jonger. Tijdens de 19de eeuw was er een beetje interesse, maar het was pas na de eeuwwisseling, met de moderne wiskundeconcepten uit de groepentheorie en de topologie, dat een echte theorie over knopen werd ontwikkeld. De twee wiskundigen die hiermee het meest geassocieerd zijn, zijn Kurt Reidemeister en James W. Alexander. Het wiskundig hoofdprobleem in de knopentheorie is aantonen dat twee knopen equivalent zijn, zeg maar twee vormen van dezelfde knoop zijn. Reidemeister toonde aan dat er maar drie transformaties of bewegingen zijn die een bestaande knoop wezenlijk niet veranderen, hoewel ze er anders uitzien. Deze bewegingen zijn: een boog draaien of terugdraaien; een boog boven of onder een andere boog halen zodat twee kruisingen ontstaan of verdwijnen; en een boog over of onder een kruising doorhalen (het aantal kruisingen verandert hier niet).

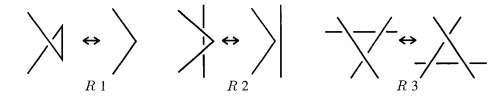
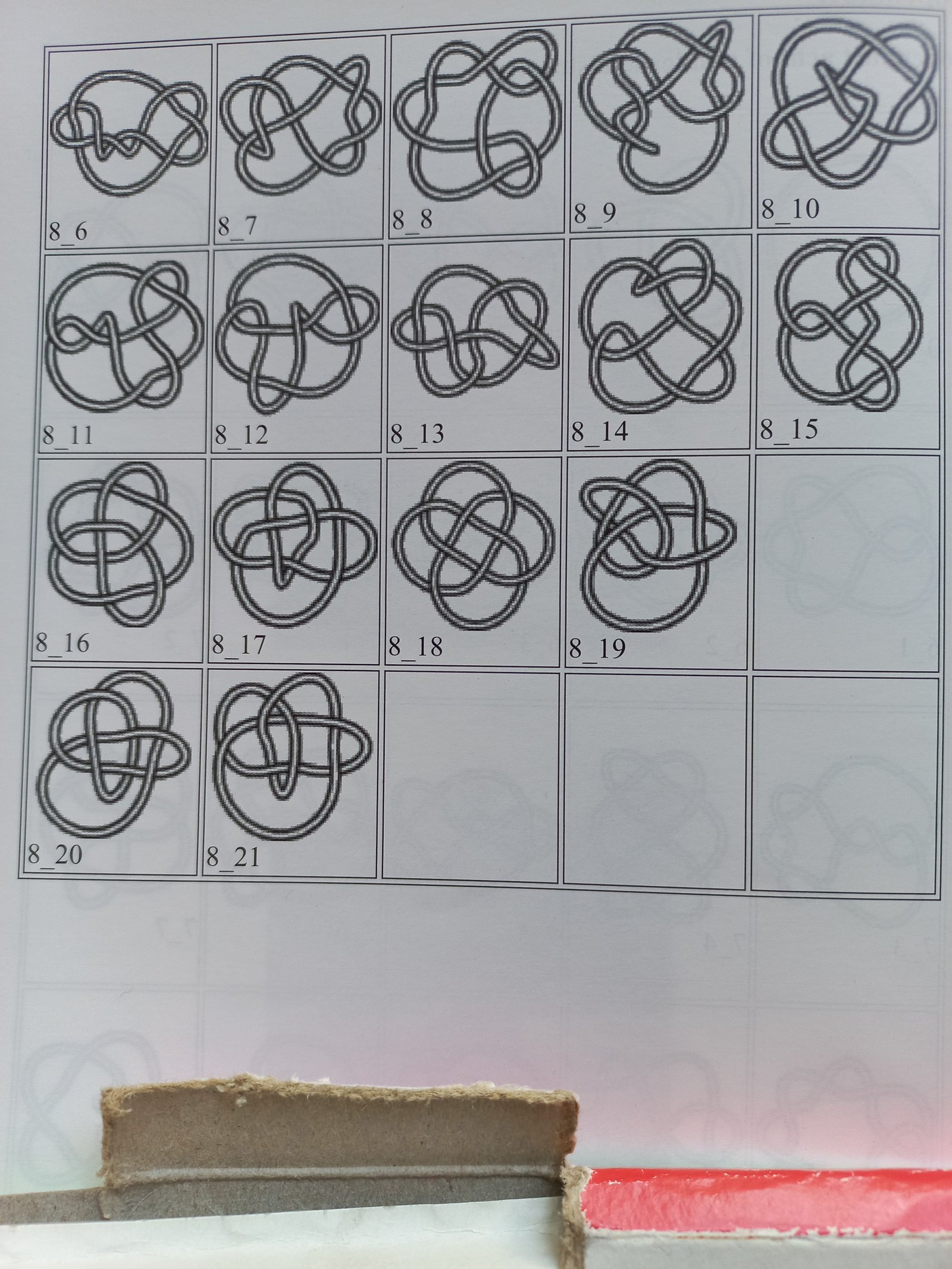
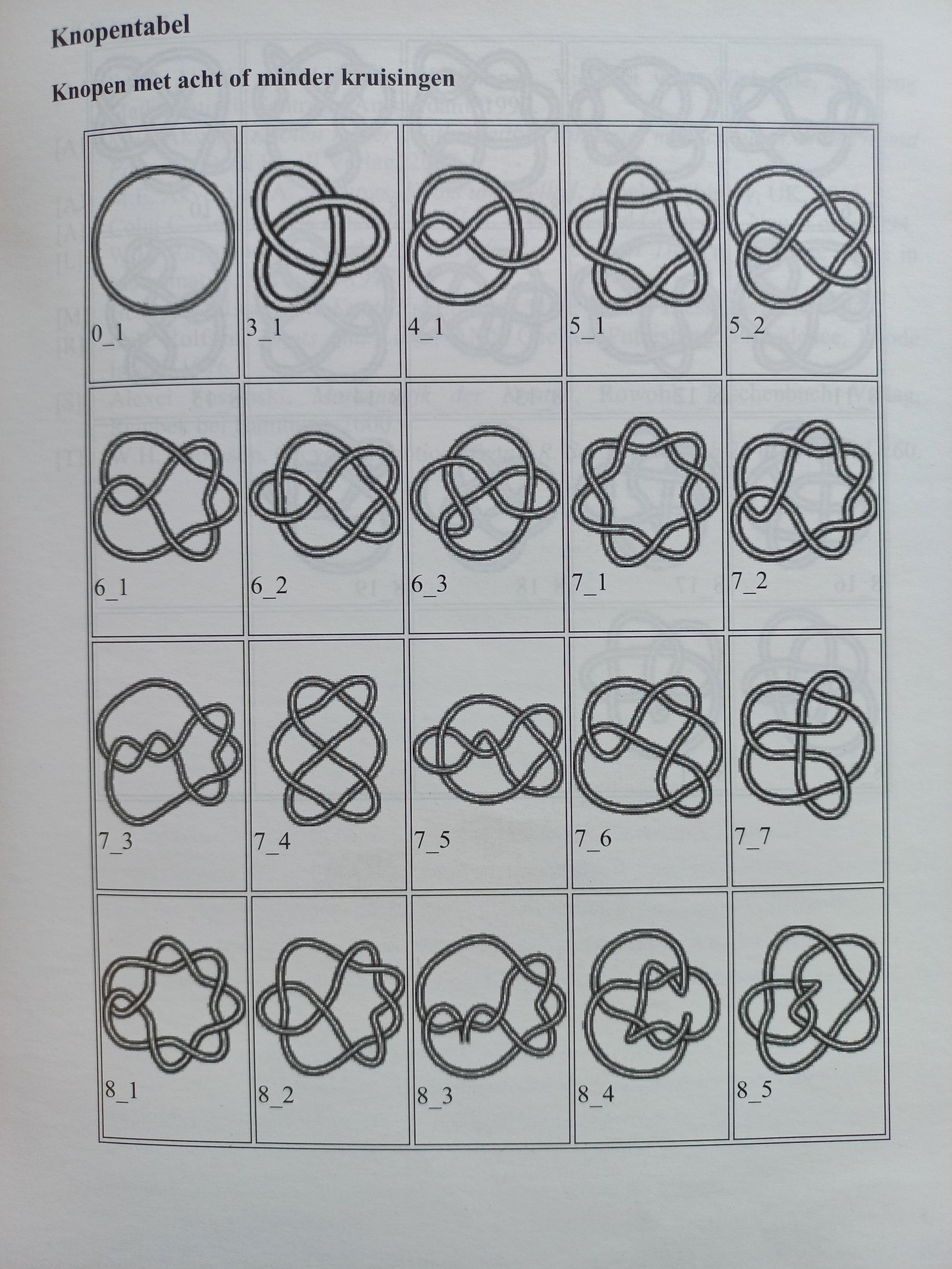
Uit deze bewegingen blijkt al: het aantal kruisingen bij knopen is cruciaal. En wiskundigen zouden geen wiskundigen zijn, zouden ze zich niet afvragen hoeveel verschillende knopen bestaan met 1 kruising, 2 kruisingen, 3 kruisingen enzoverder, of, anders gesteld, welke knopen kun je allemaal door deze bewegingen in elkaar doen overgaan en welke niet? Dit leidde uiteindelijk tot een classificatie van knopen per aantal kruisingen, de zogenaamde “priemknopen” die niet in andere knopen omgevormd kunnen worden. In de classificatie zie je de klaverbladknoop als enige knoop met 3 kruisingen, of zoals men zegt, van orde 3. Er is ook maar 1 knoop van orde 4, maar daarna zijn er meer. Bij orde 5 heb je er 2, bij orde 6 al 3, bij orde 7 zijn er 7, en bij orde 8 niet minder dan 21.