EEN DONUT IN ELKAAR STEKEN

Iedereen kent de donut als lekkernij, een rond zoet deegje met een gat in het midden.

Wiskundig gezien is de donut een torus, een ruimtelijk lichaam dat ontstaat als je het middelpunt van een cirkel (blauw) een cirkelvormige baan (rood) laat volgen. Het middelpunt van de torus is het middelpunt van die cirkelvormige baan en ligt in het midden van het gat.

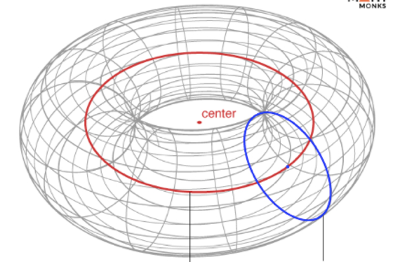
Een torus heeft veel wiskundig bijzondere eigenschappen.

• Net als bij een bol kan je elke twee punten op een torus via een cirkelsegment verbinden, zonder langs het gat te passeren.

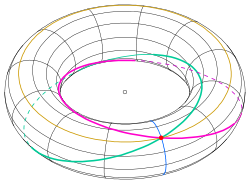
• Nevenstaande figuur illustreert de eigenschap dat door elk punt van de torus juist 4 cirkels gaan die op de torus gelegen zijn..

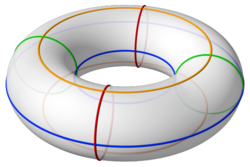
• Snijd je de bovenstaande torus horizontaal door, dan heb je twee cirkels met hetzelfde middelpunt dus concentrische cirkels (zie blauwe cirkels).

• Snijd je de torus verticaal door en door het middelpunt van het gat van de torus), dan heb je twee aparte even grote cirkels (zie rode cirkels).

• Snijd je de torus onder een hoek door, maar nog altijd door het middelpunt, dan heb je 2 snijdende cirkels met dezelfde straal, de Villarceau cirkels genoemd, naar de Franse astronoom Yvon Villarceau (1813–1883) (https://en.wikipedia.org/wiki/Villarceau_circles).

De delen van de 2 snijdende cirkels binnen de torus hebben de vorm van een maantje.

De torus die hier in elkaar wordt gestoken met 24 schijfjes papier in de vorm van een maantje, wordt terug opgebouwd vanuit Villarceau-cirkels. Net zoals je een bol in elkaar kunt steken door cirkels in elkaar te steken trouwens.