VAN BOUWPLAAT TOT 3D-VORM (ARCHIMEDISCH LICHAAM)

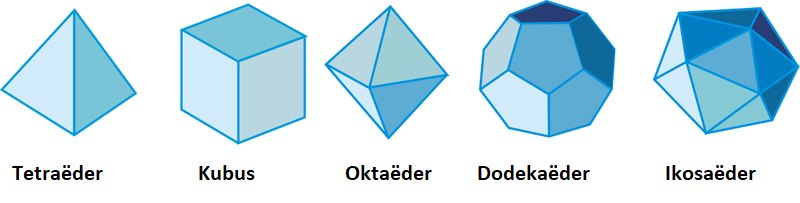
Al in de Oudheid had men zich de vraag gesteld welke ruimtelijke lichamen men kon vormen, die enkel door dezelfde regelmatige veelhoek begrensd waren. Een kubus bijvoorbeeld heeft als zijvlakken enkel regelmatige vierhoeken (vierkanten). Men vond dat er slechts vijf van die regelmatige veelvlakken, of Platonische lichamen, mogelijk waren. Dit resultaat werd door de oude Grieken als één van de hoogtepunten van de meetkunde gezien. Daarom is dit resultaat het thema van het 14de en laatste boek van Euclides’ beroemde Elementen, die de Griekse kennis van de meetkunde systematisch samenvatten.

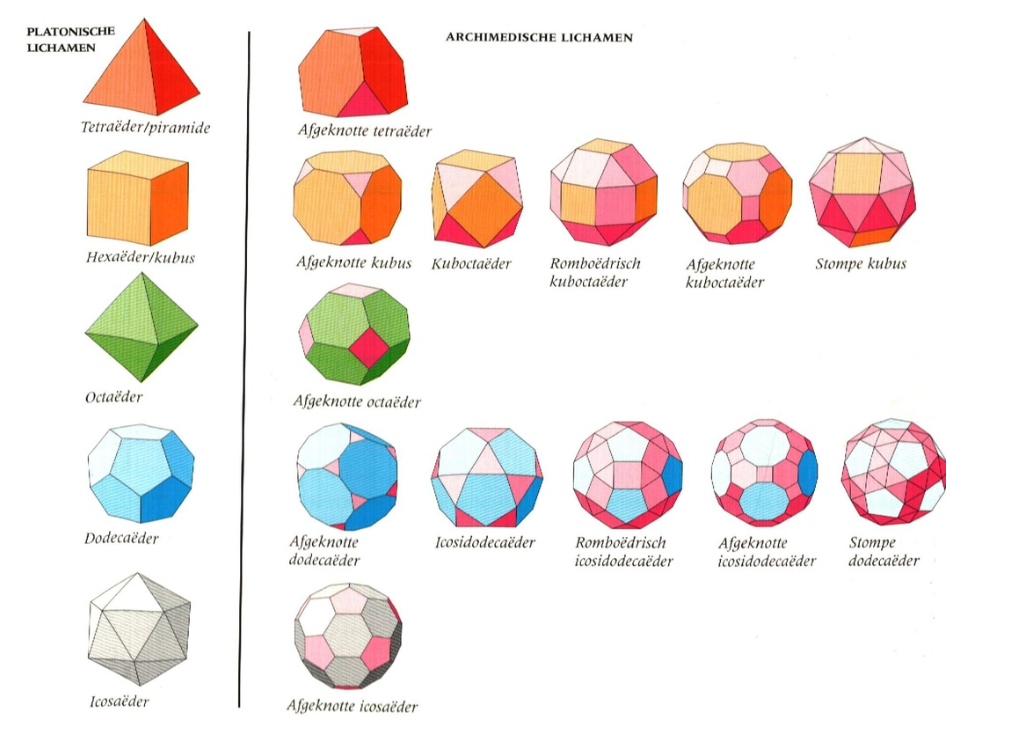
Als je een stapje verder zet, kan je je ook afvragen welke ruimtefiguren door een combinatie van verschillende regelmatige veelhoeken gevormd kunnen worden. Als je daarbij nog wil dat het ruimtelichaam ook symmetrisch is over zijn verticale en horizontale as, dan heb je de zogenaamde Archimedische lichamen, genoemd naar Archimedes, de grote Griekse wiskundige die ze als eerste beschreef. Een aantal van die lichamen kunnen gemakkelijk gevonden worden door de “punten” van Platonische lichamen af te “knippen”, dit zijn de “afgeknotte” Platonische lichamen. Ook hier vond men dat er maar een beperkt aantal mogelijk zijn, namelijk 13.

Net zoals bij alle lichamen die geen putten of stekels hebben (of die convex zijn, om de wiskundige technische term te gebruiken), geldt voor alle Platonische en Archimedische lichamen de formule van Euler. In 1750 formuleerde Leonhard Euler de volgende stelling: H+Z-R=2. Hierbij is H het aantal hoekpunten, Z het aantal zijden en R het aantal ribben van het lichaam. Als je een kubus neemt dan heb je 8 hoekpunten, 6 zijden en 12 ribben, dus 8+6-12 is inderdaad 2.

1. Als je de horizontale of verticale symmetrie laat varen, dan heb je nog twee andere groepen van halfregelmatige veelvlakken, namelijk prisma’s en antiprisma’s.

2. Een convex lichaam is een lichaam waar elk lijnstuk waarmee je twee willekeurige punten van het lichaam verbindt, volledig binnen het lichaam ligt. In het geval van een ster met stekels bijvoorbeeld is het lijnstuk dat twee sterpunten verbindt niet binnenin de ster. Heb je een bal met een putje erin, dan is een lijnstuk dat twee punten van de put verbindt ook niet binnen de bal.